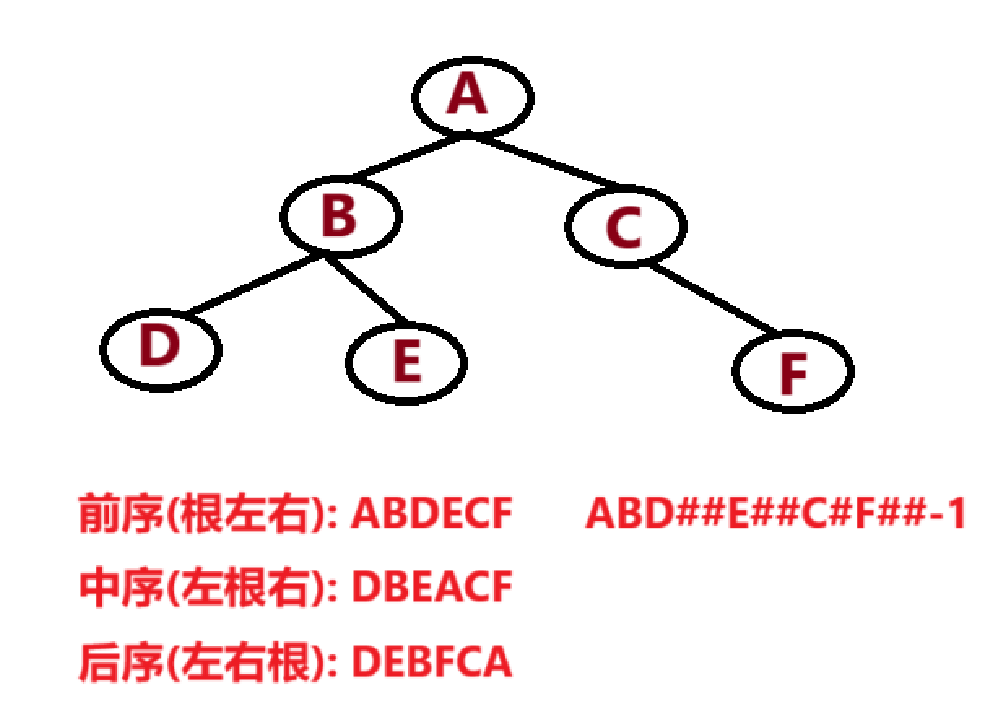
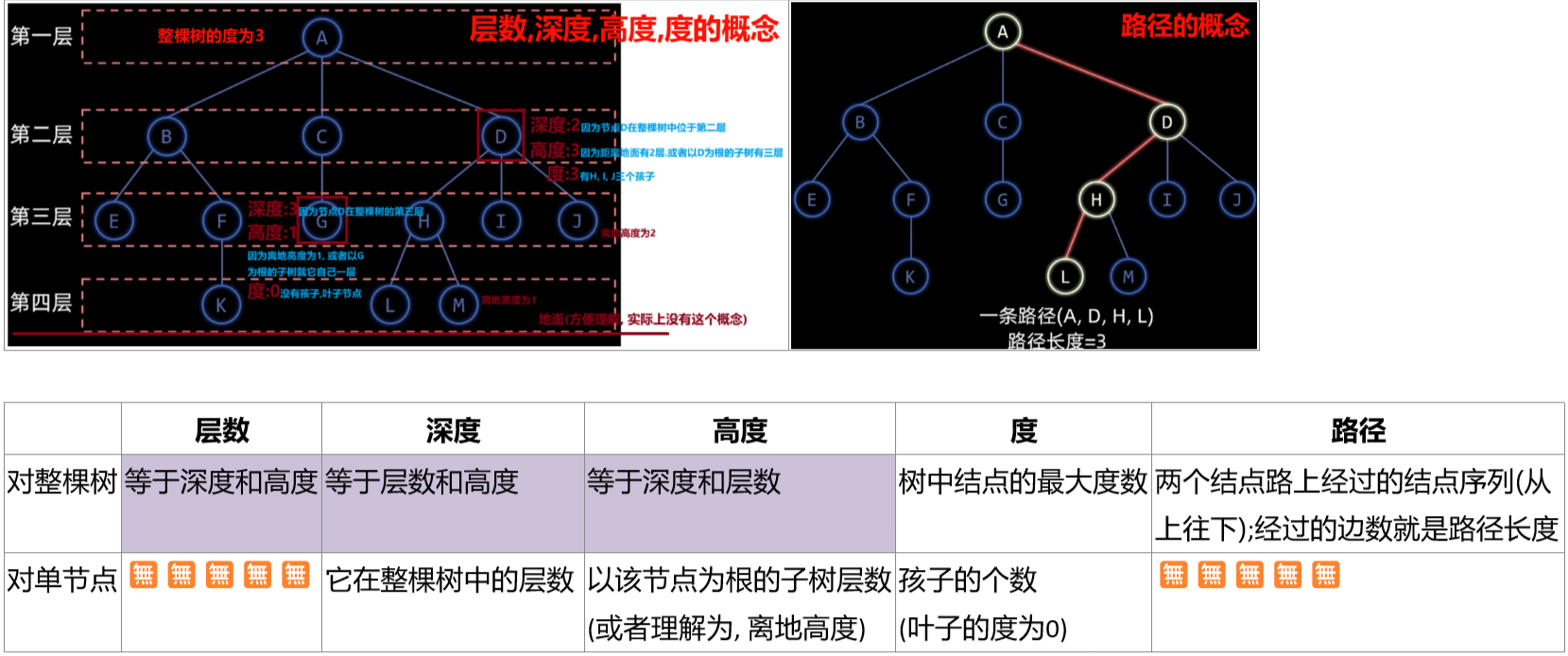
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
| #include "tree.h"
void createTree(TreeNode **tree) {
char input;
while (scanf("%c", &input) == 1 && input != '\n') {
if (input == '#') {
*tree = NULL;
return;
} else {
TreeNode *newNode = (TreeNode *)malloc(sizeof(TreeNode));
newNode->data = input;
newNode->lchild = NULL;
newNode->rchild = NULL;
*tree = newNode;
createTree(&(*tree)->lchild);
createTree(&(*tree)->rchild);
return;
}
}
}
void preOrder(TreeNode *tree) {
if (tree != NULL) {
printf("%c ", tree->data);
preOrder(tree->lchild);
preOrder(tree->rchild);
}
}
void inOrder(TreeNode *tree) {
if (tree != NULL) {
inOrder(tree->lchild);
printf("%c ", tree->data);
inOrder(tree->rchild);
}
}
void postOrder(TreeNode *tree) {
if (tree != NULL) {
postOrder(tree->lchild);
postOrder(tree->rchild);
printf("%c ", tree->data);
}
}
TreeNode *stack[SIZE];
int top = -1;
void preOrderWithStack(TreeNode *tree) {
top = -1;
TreeNode *pmove = tree;
while (top != -1 || pmove != NULL) {
if (pmove == NULL) {
pmove = stack[top--]->rchild;
}
else {
printf("%c ", pmove->data);
stack[++top] = pmove;
pmove = pmove->lchild;
}
}
}
void inOrderWithStack(TreeNode *tree) {
top = -1;
TreeNode *pmove = tree;
while (top != -1 || pmove != NULL) {
if (pmove == NULL) {
printf("%c ", stack[top]->data);
pmove = stack[top--]->rchild;
}
else {
stack[++top] = pmove;
pmove = pmove->lchild;
}
}
}
void postOrderWithStack(TreeNode *tree) {
top = -1;
TreeNode *pmove = tree;
char printStack[100];
int pTop = -1;
while (top != -1 || pmove != NULL) {
if (pmove == NULL) {
pmove = stack[top--]->lchild;
} else {
printStack[++pTop] = pmove->data;
stack[++top] = pmove;
pmove = pmove->rchild;
}
}
while (pTop != -1) {
printf("%c ", printStack[pTop--]);
}
}
TreeNode *queue[SIZE];
int hh = 0, tt = -1;
void levelOrder(TreeNode *tree) {
hh = 0, tt = -1;
queue[++tt] = tree;
while (hh <= tt) {
TreeNode *temp = queue[hh++];
printf("%c ", temp->data);
if (temp->lchild != NULL) {
queue[++tt] = temp->lchild;
}
if (temp->rchild != NULL) {
queue[++tt] = temp->rchild;
}
}
}
|