13.树【红黑树RBT】

13.树【红黑树RBT】

明廷盛 嘻嘻😁
  2025-04-07 10:20:47 2025-04-07 10:20:47 Created   2025-04-08 15:21 2025-04-08 15:21 Updated   2.5k Words  11 Mins  

第一章 自测&关键词回顾

理论:①四个性质 ②如何变色 ③如何旋转 ④如何删除
实现:有头节点的三叉树 GCC红黑树实现
参考: 视频

  • 大体思路:
    • 头节点的parent域存储整棵树的根; data域表示为-1(或其他值/或你标识颜色也OK,更为保险); lrchild都不存东西;
    • 这样维护, 在LRotation和RRotation时, 会方便维护parent节点; ==无需传递二级指针, 换根, 直接parent->l/rchild换即可==

第一节 红黑树的四个性质

  • 四个性质:
    1. ① 是BST
    2. ②【根叶黑】根和叶子(NULL)必须是黑色
    3. ③【不红红】不存在连续的两个红色节点
    4. ④【黑路同】任意节点到叶子🍃所有路径,经过的黑色结点数量相同
  • 两个结论:
    • 从”整棵树”根到叶🍃的最长路径(尽可能多的红)<= 2* (“整棵树”根到叶🍃的最短路径(全黑)) 【因为“不红红”所以最长的路径上，红和黑节点个数相同】

      为什么维护这四个性质能使得”红黑树”在增删改的速度变快? 红黑树对比AVL的优势是什么? 视频

第二节 如何旋转

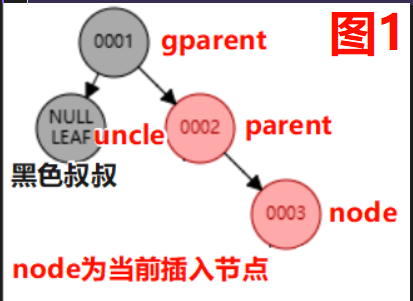
理论: 我们在插入的时候, 会有以下三种情况；其中只有case3与旋转有关; 节点说明如“图1”所示
实现: L/RRotation需要维护parent节点; 同时也需要维护parent到该节点(双向维护)

case1: 插入节点是根节点【违反 根叶黑】

调整方法: 根节点变黑

case2:插入节点的叔叔是红色【违反 不红红】

调整方法: ①gparent变为红色(1)，parent和uncle变为黑色(0) ②让gparent节点变为插入的节点,继续向上检查

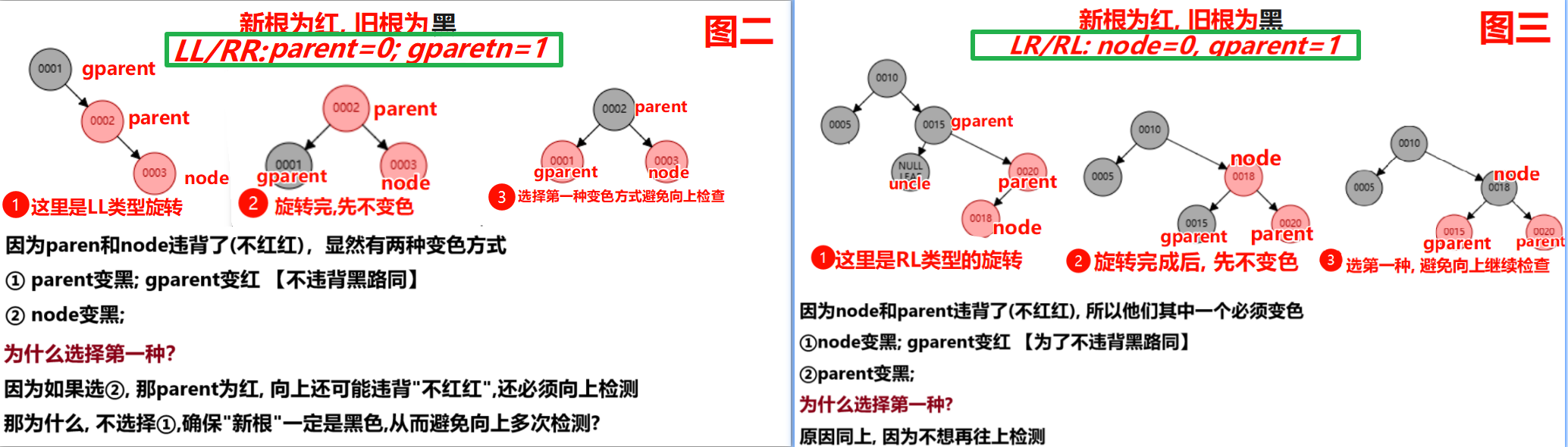
case3:插入节点的叔叔是黑色【违反 不红红】

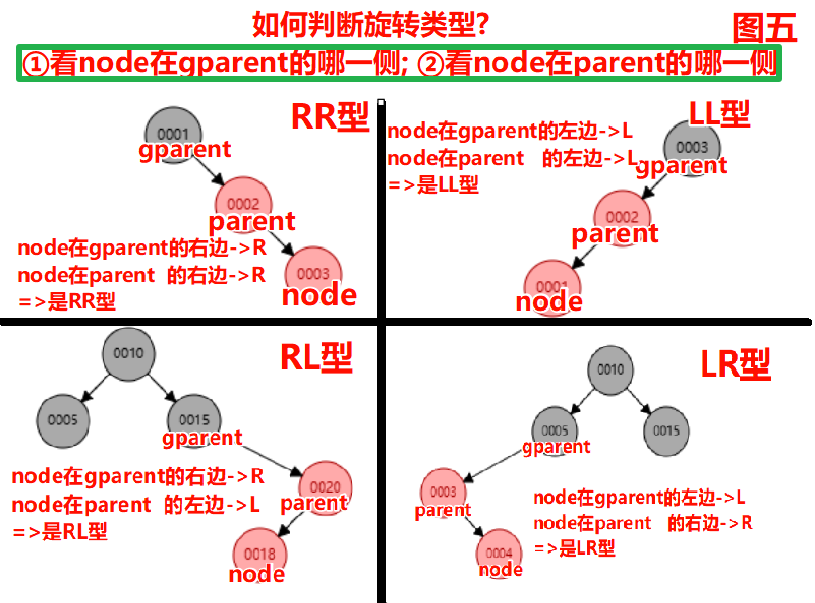
调整方法: ①新根为黑色; 原根为红色 ②以node在gparetn和parent的位置;判断旋转类型

  • 可见判断旋转类型, 无需通过平衡因子, 所以可以不维护height属性
    |675

第三节 如何变色

我们在插入的时候, 会有以下三种情况；这里重点解释调整时的变色; 节点说明如“图1”所示

case1: 插入节点是根节点【违反 根叶黑】

调整方法: 根节点变黑

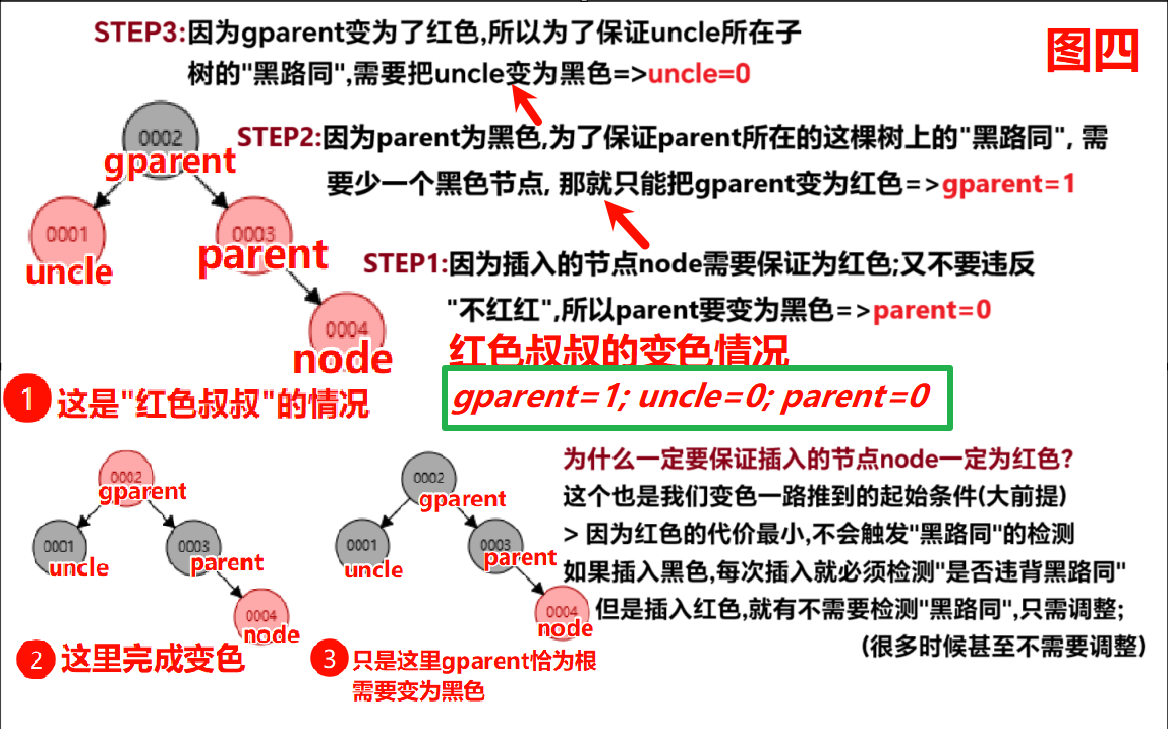
case2:插入节点的叔叔是红色【违反 不红红】

调整方法: ①gparent变为红色(1)，parent和uncle变为黑色(0) ②让gparent节点变为插入的节点,继续向上检查

|625

case3:插入节点的叔叔是黑色【违反 不红红】

调整方法: ①新根为黑色; 原根为红色 ②以node在gparetn和parent的位置;判断旋转类型

  • 如何判断是否违背”黑路同”? 引入天外节点, 进行判断

第四节 如何实现”插入”方法

本质还是BST; 需要以下方法①BST插入(但要返回新增节点) ②fixRBTree(传入新节点):用于维护红黑树的性质 ③RRotation()和LRotation(): 用于旋转

1
2
3
4
5
6
7
8
9
10
11
// 1.初始化红黑树
TreeNode *init(int *input, int length) {
    TreeNode *head = (TreeNode *)malloc(sizeof(TreeNode));
    head->parent = NULL;
    head->data = -1;  // 哨兵头的值域为-1
    for (int i = 0; i < length; i++) {
        TreeNode *newNod = insert(&(head->parent), *(input + i), head);
        fixRBTree(head->parent, newNod);
    }
    return head;
}

1.4.1 BST插入(但要返回新增节点)

和BST一样: 只是需要返回新节点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/** 2.插入
 *  TreeNode **root:整棵树的根
 *  int x: 插入的值
 *  :return
 *      返回新插入的节点
 */
TreeNode *insert(TreeNode **root, int x, TreeNode *parent) {
    if (*root == NULL) {
        TreeNode *newNode = (TreeNode *)malloc(sizeof(TreeNode));
        newNode->data = x;
        newNode->color = 1; // 新插入的节点必须是红色(代价最小)
        newNode->lchild = newNode->rchild = NULL;
        newNode->parent = parent;

        *root = newNode;
        return newNode;
    } else if (x < (*root)->data) {
        return insert(&(*root)->lchild, x, *root);
    } else {
        return insert(&(*root)->rchild, x, *root);
    }
}

1.4.2 fixRBTree(传入新节点)

关键方法: 用于维护红黑树的性质

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
/**  2-1 修复红黑树
 * TreeNode *root:整棵树的根
 * TreeNode *node:新插入的节点
 */
void fixRBTree(TreeNode *root, TreeNode *node) {
    TreeNode *newNode = root;
    while (node->data != newNode->data) {
        newNode = node->data < newNode->data ? newNode->lchild : newNode->rchild;
    }
    while (newNode->parent->data != -1 && newNode->parent->color == 1) {
        // 开始修复
        TreeNode *parent = newNode->parent;
        TreeNode *gparent = parent->parent;
        TreeNode *uncle = gparent->lchild == parent ? gparent->rchild : gparent->lchild;
        int uncleColor = uncle ? uncle->color : 0;

        // 红色叔叔
        if (uncleColor == 1) {
            parent->color = 0;
            gparent->color = 1;
            uncle->color = 0;
            newNode = gparent;
            continue;
        }
        // 黑色叔叔
        else {
            if (parent->data < gparent->data) {
                if (newNode->data < parent->data) {
                    // LL
                    parent->color = 0;
                    gparent->color = 1;
                    RRotation(gparent);
                } else {
                    // LR
                    newNode->color = 0;
                    gparent->color = 1;
                    LRotation(gparent->lchild);
                    RRotation(gparent);
                }
            } else {
                if (newNode->data < parent->data) {
                    // RL
                    newNode->color = 0;
                    gparent->color = 1;
                    RRotation(gparent->rchild);
                    LRotation(gparent);
                } else {
                    // RR
                    parent->color = 0;
                    gparent->color = 1;
                    LRotation(gparent);
                }
            }
            break;  // 必须有
        }
    }

    root->color = 0;  // 保证根叶黑
}

1.4.3 RRotation和LRotation(需要维护parent)

因为”红黑树”有parent,需要相较于AVL, 需要维护下parent即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
// 左旋
void LRotation(TreeNode *tree) {
    /** 变量定义
     *     1(root)
     *      \
     *       2(rRChild)
     *     /    \
     *    /      \
     *  0(orphan)  3
     *
     */
    TreeNode *root = tree;
    TreeNode *rRChild = root->rchild;
    TreeNode *orphan = rRChild->lchild;
    TreeNode *outerNode = root->parent;  // 一定存在, 因为有哨兵头

    /** 旋转
     *      2(rRChild)
     *    /   \
     *   /     \
     *  1(root) 3
     *    \
     *     \
     *      0 (orphan)
     */
    rRChild->lchild = root;
    root->rchild = orphan;

    /** 父节点修正
     *   X(outerNode)
     *    ③
     *     ③双向修正
     *      2(rRChild)
     *    ②   \
     *   /     \
     *  1(root) 3
     *    ①
     *     \
     *      0 (orphan)
     */
    if (orphan)
        orphan->parent = root;    // ①
    root->parent = rRChild;       // ②
    rRChild->parent = outerNode;  // ③
    if (outerNode->data == -1) {  // 哨兵头
        outerNode->parent = rRChild;
    } else {
        if (outerNode->lchild == root) {
            outerNode->lchild = rRChild;
        } else {
            outerNode->rchild = rRChild;
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
// 右旋
void RRotation(TreeNode *tree) {
    /** 变量定义
     *     1(root)
     *     /
     *    2(rLChild)
     *   /   \
     *  3     0(orphan)
     *
     */
    TreeNode *root = tree;
    TreeNode *rLChild = root->lchild;  // (rootLeftChild)
    TreeNode *orphan = rLChild->rchild;
    TreeNode *outerNode = root->parent;

    /** 旋转
     *    2(rLChild)
     *   /   \
     *  3    1(root)
     *        /
     *     0(orphan)
     */
    rLChild->rchild = root;
    root->lchild = orphan;

    /** 父节点修正
     *   X(outerNode)
     *    ③
     *     ③双向修正
     *     2(rLChild)
     *     / ②
     *    /   \
     *   3    1(root)
     *        ①
     *        /
     *     0(orphan)
     */
    if (orphan)
        orphan->parent = root;    // ①
    root->parent = rLChild;       // ②
    rLChild->parent = outerNode;  // ③
    if (outerNode->data == -1) {
        outerNode->parent = rLChild;
    } else {
        if (outerNode->lchild == root) {
            outerNode->lchild = rLChild;
        } else {
            outerNode->rchild = rLChild;
        }
    }
}

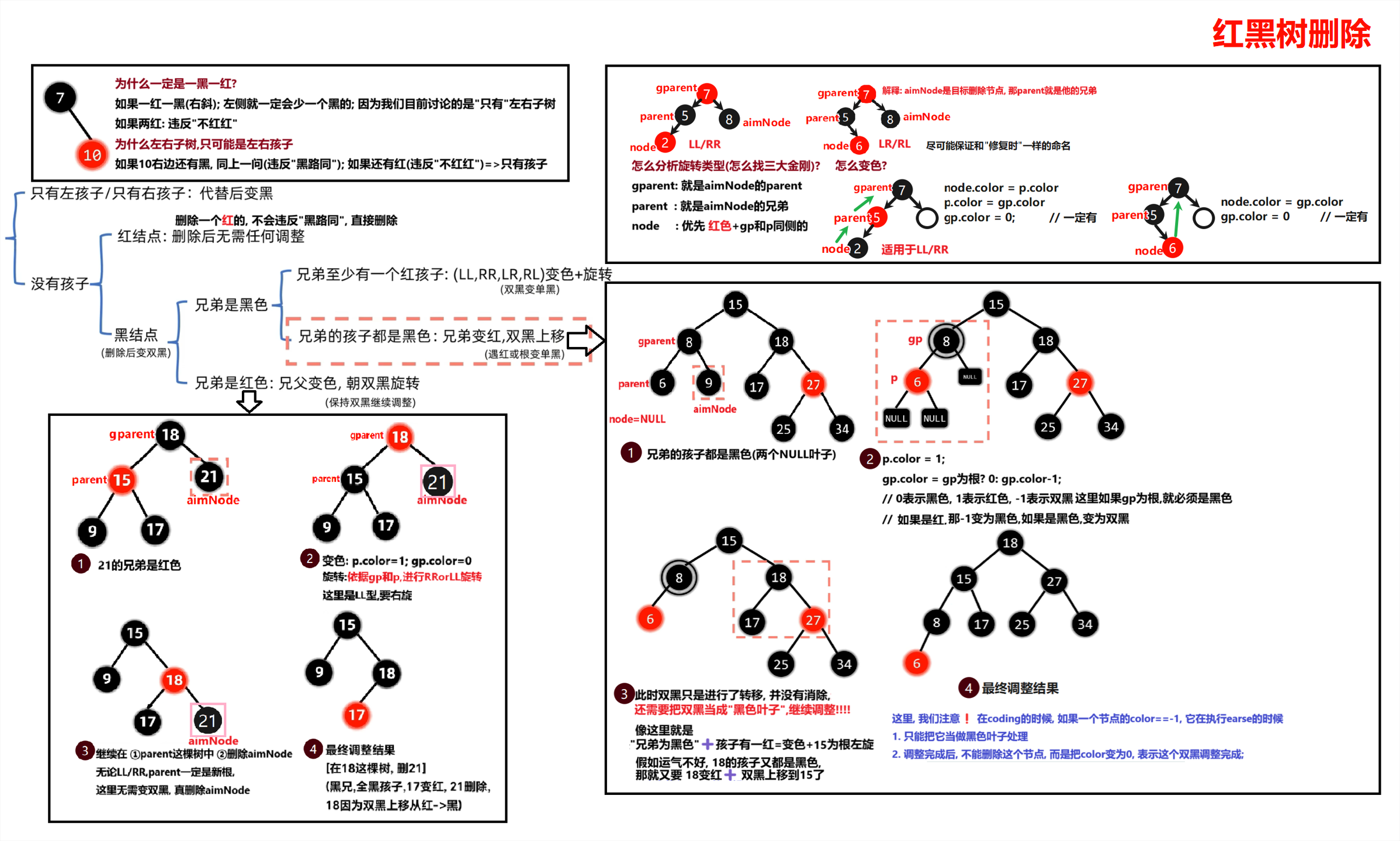
第五节 红黑树删除

这部分要推导比较困难(主播是笨蛋!),建议直接记住;

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
// 3.删除
void earse(TreeNode *root, int x) {
    TreeNode *aimNode = root;
    while (x != aimNode->data) {
        aimNode = x < aimNode->data ? aimNode->lchild : aimNode->rchild;
    }

    // case1: 叶子节点🍃
    if ((aimNode->lchild == NULL && aimNode->rchild == NULL) || aimNode->color == -1) {
        if (aimNode->parent->data == -1) {  // 细品(当前节点时根节点+当前节点是叶子==>整棵树只有一个根)
            aimNode->parent->parent = NULL;
            return;
        }
        // case1-1: 黑色叶子
        if (aimNode->color != 1) {
            /**  左侧情况 变量标识
             *   有两孩?优先左       没有左?就等于右       没有右,那为NULL
             *      a(gp)             a(gp)              a(gp)
             *     /  \              /   \               /   \
             *   b(p)  c(aimNode)   b(p)  c(aimNode)   b(p)  c(aimNode)
             *   /  \                 \
             * c(n) d                 c(n)               node=NULL
             */
            TreeNode *gparent = aimNode->parent;
            TreeNode *parent = gparent->lchild == aimNode ? gparent->rchild : gparent->lchild;
            TreeNode *node = NULL;
            if (parent == gparent->lchild) {
                if (parent->lchild && parent->lchild->color == 1)  //  优先同侧孩子
                    node = parent->lchild;
                else if (parent->rchild && parent->rchild->color == 1)
                    node = parent->rchild;

            } else {
                if (parent->rchild && parent->rchild->color == 1)  //  优先同侧孩子
                    node = parent->rchild;
                else if (parent->lchild && parent->lchild->color == 1)
                    node = parent->lchild;
            }

            // case1-2-1: aimNode兄弟为红色=>兄弟变为黑色;父亲变为红色;依据兄弟和父亲进行旋转;然后继续删除aimNode所在的树
            if (parent->color == 1) {
                parent->color = 0;
                gparent->color = 1;
                if (gparent->lchild == parent) {
                    // LL
                    RRotation(gparent);
                } else {
                    // RR
                    LRotation(gparent);
                }
                earse(parent, x);
                return;
            }
            // case1-2-2: aimNode的兄弟为黑色
            else {
                // 至少有一个红孩
                if (node != NULL) {
                    if (parent->data < gparent->data) {
                        if (node->data < parent->data) {
                            // LL
                            node->color = parent->color;
                            parent->color = gparent->color;
                            gparent->color = 0;
                            RRotation(gparent);
                        } else {
                            // LR
                            node->color = gparent->color;
                            gparent->color = 0;
                            LRotation(parent);
                            RRotation(gparent);
                        }
                    } else {
                        if (node->data < parent->data) {
                            // RL
                            node->color = gparent->color;
                            gparent->color = 0;
                            RRotation(parent);
                            LRotation(gparent);
                        } else {
                            // RR
                            node->color = parent->color;
                            parent->color = gparent->color;
                            gparent->color = 0;
                            LRotation(gparent);
                        }
                    }
                }
                // 一个红色孩子都没有
                else {
                    parent->color = 1;
                    gparent->color = gparent->parent->data == -1 ? 0 : gparent->color - 1;  // -1表示双黑,如果是根就为黑,红(1)--,也变为黑
                    if (gparent->color == -1)
                        earse(root, gparent->data);  // 双黑上移=继续删除gp的值 + 假删除
                }
            }
        }
        // case1-1: 红色叶子,直接删除,这条路上的黑色不会变化(不违反黑路同)
        if (aimNode->color != -1) {  // 如果是-1,表示为假删
            if (aimNode->parent->lchild == aimNode) // 注意删节点的方式: 和没有哨兵头的区别
                aimNode->parent->lchild = NULL;
            else
                aimNode->parent->rchild = NULL;
        } else {
            aimNode->color = 0;  // 修复为黑色即可
        }

    }
    // case2: 有两个孩子
    else if (aimNode->lchild != NULL && aimNode->rchild != NULL) {
        // 找到"中序遍历"的后继节点 (aimNode右子树的最左边节点)
        TreeNode *successor = aimNode->rchild;
        while (successor->lchild) {
            successor = successor->lchild;
        }
        // 换值(真, 因为只有真换值,才能保证aimNode的右子树是BST,才能使用earse方法继续删除)
        aimNode->data = aimNode->data ^ successor->data;
        successor->data = aimNode->data ^ successor->data;
        aimNode->data = aimNode->data ^ successor->data;

        // 删除右子树上的x
        earse(aimNode->rchild, x);

    }
    // case3: 只有一个孩子
    else {
        TreeNode *outerNode = aimNode->parent;
        TreeNode *son = aimNode->lchild ? aimNode->lchild : aimNode->rchild;
        // 修改颜色
        son->color = 0;  // 一红一黑; 用红替换了黑的,会少一个黑的,所以得替换
        // 修复父节点关系
        if (outerNode->lchild == aimNode) {
            outerNode->lchild = son;
        } else {
            outerNode->rchild = son;
        }
        son->parent = outerNode;  // 修改父子,双向修改
        // 替换 (没必要了, 修正父节点的子节点即可, 相当于完成替换了)
    }
}

第二章 手撕

第三章 相关应用

第四章 上手真题

第五章 比赛怎么用

  • Title: 13.树【红黑树RBT】
  • Author: 明廷盛
  • Created at : 2025-04-07 10:20:47
  • Updated at : 2025-04-08 15:21:00
  • Link: https://blog.20040424.xyz/2025/04/07/🏫考研/第一部分 数据结构/13.树【红黑树RBT】/
  • License: All Rights Reserved © 明廷盛
On this page
13.树【红黑树RBT】
  1. 第一章 自测&关键词回顾
    1. 第一节 红黑树的四个性质
    2. 第二节 如何旋转
    3. 第三节 如何变色
    4. 第四节 如何实现”插入”方法
    5. 第五节 红黑树删除
  2. 第二章 手撕
  3. 第三章 相关应用
  4. 第四章 上手真题
  5. 第五章 比赛怎么用