13.树【红黑树RBT】

第一章 自测&关键词回顾

理论:①四个性质 ②如何变色 ③如何旋转 ④如何删除
实现:有头节点的三叉树 GCC红黑树实现
参考: 视频

• 大体思路:
  • 头节点的parent域存储整棵树的根; data域表示为-1(或其他值/或你标识颜色也OK,更为保险); lrchild都不存东西;
  • 这样维护, 在LRotation和RRotation时, 会方便维护parent节点; ==无需传递二级指针, 换根, 直接parent->l/rchild换即可==

第一节 红黑树的四个性质

• 四个性质:
  1. ① 是BST
  2. ②【根叶黑】根和叶子(NULL)必须是黑色
  3. ③【不红红】不存在连续的两个红色节点
  4. ④【黑路同】任意节点到叶子🍃所有路径,经过的黑色结点数量相同
• 两个结论:
  • 从”整棵树”根到叶🍃的最长路径(尽可能多的红)<= 2* (“整棵树”根到叶🍃的最短路径(全黑)) 【因为“不红红”所以最长的路径上，红和黑节点个数相同】

    为什么维护这四个性质能使得”红黑树”在增删改的速度变快? 红黑树对比AVL的优势是什么? 视频

第二节 如何旋转

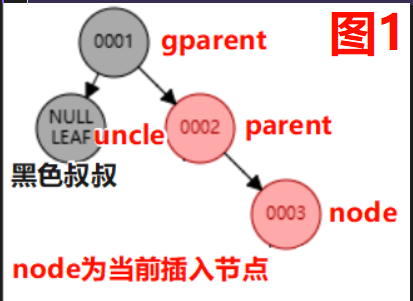
理论: 我们在插入的时候, 会有以下三种情况；其中只有case3与旋转有关; 节点说明如“图1”所示
实现: L/RRotation需要维护parent节点; 同时也需要维护parent到该节点(双向维护)

case1: 插入节点是根节点【违反 根叶黑】

调整方法: 根节点变黑

case2:插入节点的叔叔是红色【违反 不红红】

调整方法: ①gparent变为红色(1)，parent和uncle变为黑色(0) ②让gparent节点变为插入的节点,继续向上检查

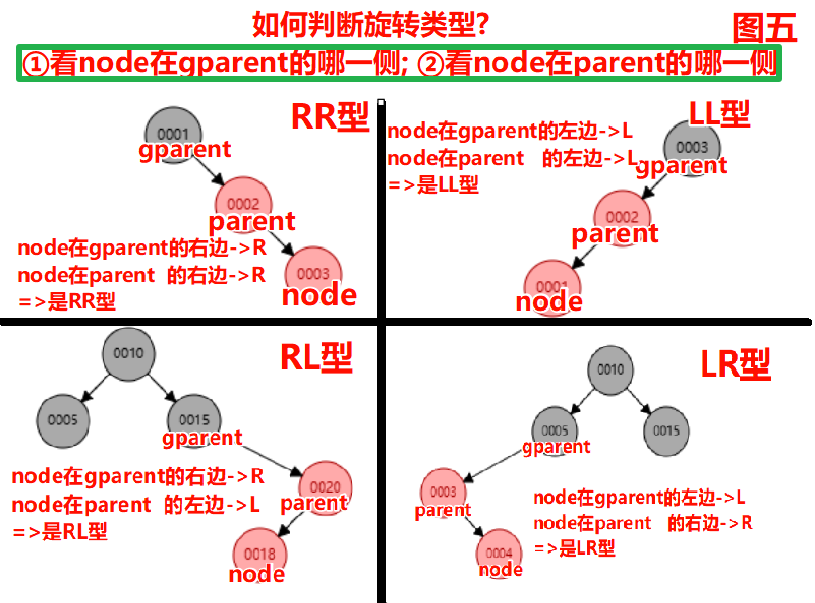
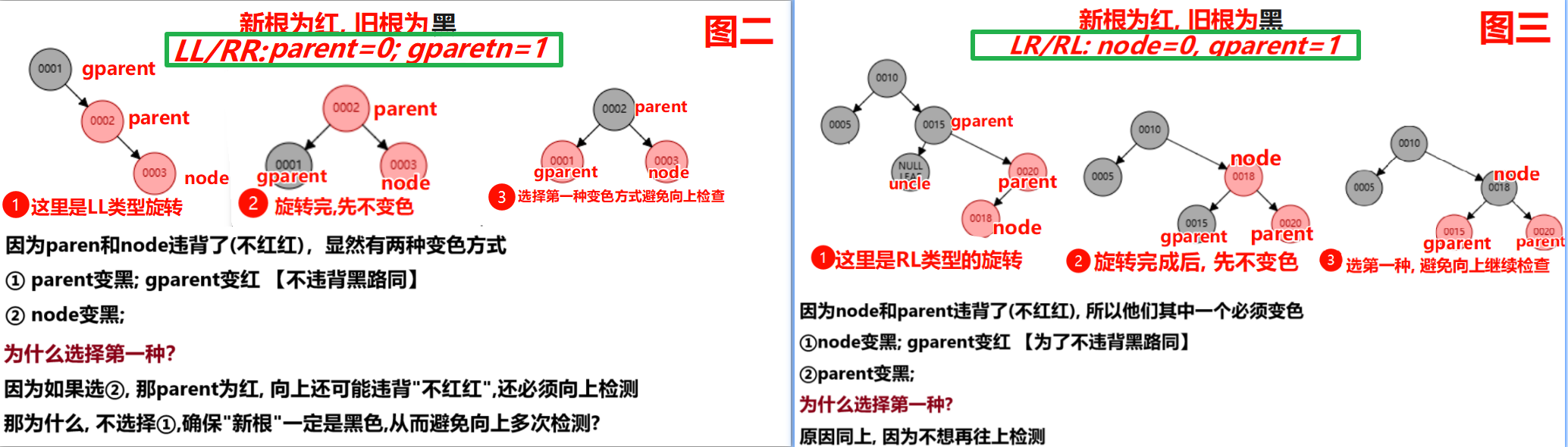
case3:插入节点的叔叔是黑色【违反 不红红】

调整方法: ①新根为黑色; 原根为红色 ②以node在gparetn和parent的位置;判断旋转类型

• 可见判断旋转类型, 无需通过平衡因子, 所以可以不维护height属性
  

第三节 如何变色

我们在插入的时候, 会有以下三种情况；这里重点解释调整时的变色; 节点说明如“图1”所示

case1: 插入节点是根节点【违反 根叶黑】

调整方法: 根节点变黑

case2:插入节点的叔叔是红色【违反 不红红】

调整方法: ①gparent变为红色(1)，parent和uncle变为黑色(0) ②让gparent节点变为插入的节点,继续向上检查

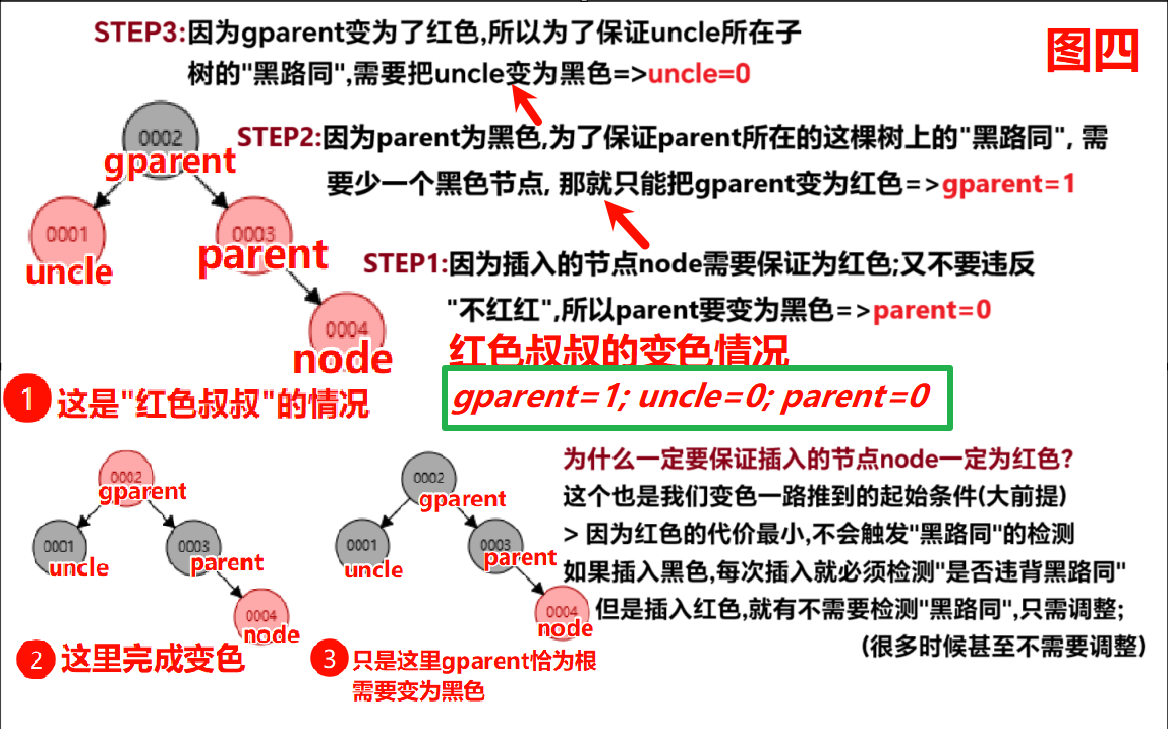
case3:插入节点的叔叔是黑色【违反 不红红】

调整方法: ①新根为黑色; 原根为红色 ②以node在gparetn和parent的位置;判断旋转类型

• 如何判断是否违背”黑路同”? 引入天外节点, 进行判断
  

第四节 如何实现”插入”方法

本质还是BST; 需要以下方法①BST插入(但要返回新增节点) ②fixRBTree(传入新节点):用于维护红黑树的性质 ③RRotation()和LRotation(): 用于旋转

// 1.初始化红黑树
TreeNode *init(int *input, int length) {
    TreeNode *head = (TreeNode *)malloc(sizeof(TreeNode));
    head->parent = NULL;
    head->data = -1;  // 哨兵头的值域为-1
    for (int i = 0; i < length; i++) {
        TreeNode *newNod = insert(&(head->parent), *(input + i), head);
        fixRBTree(head->parent, newNod);
    }
    return head;
}

1.4.1 BST插入(但要返回新增节点)

和BST一样: 只是需要返回新节点

/** 2.插入
 *  TreeNode **root:整棵树的根
 *  int x: 插入的值
 *  :return
 *      返回新插入的节点
 */
TreeNode *insert(TreeNode **root, int x, TreeNode *parent) {
    if (*root == NULL) {
        TreeNode *newNode = (TreeNode *)malloc(sizeof(TreeNode));
        newNode->data = x;
        newNode->color = 1; // 新插入的节点必须是红色(代价最小)
        newNode->lchild = newNode->rchild = NULL;
        newNode->parent = parent;

        *root = newNode;
        return newNode;
    } else if (x < (*root)->data) {
        return insert(&(*root)->lchild, x, *root);
    } else {
        return insert(&(*root)->rchild, x, *root);
    }
}

1.4.2 fixRBTree(传入新节点)

关键方法: 用于维护红黑树的性质

/**  2-1 修复红黑树
 * TreeNode *root:整棵树的根
 * TreeNode *node:新插入的节点
 */
void fixRBTree(TreeNode *root, TreeNode *node) {
    TreeNode *newNode = root;
    while (node->data != newNode->data) {
        newNode = node->data < newNode->data ? newNode->lchild : newNode->rchild;
    }
    while (newNode->parent->data != -1 && newNode->parent->color == 1) {
        // 开始修复
        TreeNode *parent = newNode->parent;
        TreeNode *gparent = parent->parent;
        TreeNode *uncle = gparent->lchild == parent ? gparent->rchild : gparent->lchild;
        int uncleColor = uncle ? uncle->color : 0;

        // 红色叔叔
        if (uncleColor == 1) {
            parent->color = 0;
            gparent->color = 1;
            uncle->color = 0;
            newNode = gparent;
            continue;
        }
        // 黑色叔叔
        else {
            if (parent->data < gparent->data) {
                if (newNode->data < parent->data) {
                    // LL
                    parent->color = 0;
                    gparent->color = 1;
                    RRotation(gparent);
                } else {
                    // LR
                    newNode->color = 0;
                    gparent->color = 1;
                    LRotation(gparent->lchild);
                    RRotation(gparent);
                }
            } else {
                if (newNode->data < parent->data) {
                    // RL
                    newNode->color = 0;
                    gparent->color = 1;
                    RRotation(gparent->rchild);
                    LRotation(gparent);
                } else {
                    // RR
                    parent->color = 0;
                    gparent->color = 1;
                    LRotation(gparent);
                }
            }
            break;  // 必须有
        }
    }

    root->color = 0;  // 保证根叶黑
}

1.4.3 RRotation和LRotation(需要维护parent)

因为”红黑树”有parent,需要相较于AVL, 需要维护下parent即可

• LRotation
• RRotation

// 左旋
void LRotation(TreeNode *tree) {
    /** 变量定义
     *     1(root)
     *      \
     *       2(rRChild)
     *     /    \
     *    /      \
     *  0(orphan)  3
     *
     */
    TreeNode *root = tree;
    TreeNode *rRChild = root->rchild;
    TreeNode *orphan = rRChild->lchild;
    TreeNode *outerNode = root->parent;  // 一定存在, 因为有哨兵头

    /** 旋转
     *      2(rRChild)
     *    /   \
     *   /     \
     *  1(root) 3
     *    \
     *     \
     *      0 (orphan)
     */
    rRChild->lchild = root;
    root->rchild = orphan;

    /** 父节点修正
     *   X(outerNode)
     *    ③
     *     ③双向修正
     *      2(rRChild)
     *    ②   \
     *   /     \
     *  1(root) 3
     *    ①
     *     \
     *      0 (orphan)
     */
    if (orphan)
        orphan->parent = root;    // ①
    root->parent = rRChild;       // ②
    rRChild->parent = outerNode;  // ③
    if (outerNode->data == -1) {  // 哨兵头
        outerNode->parent = rRChild;
    } else {
        if (outerNode->lchild == root) {
            outerNode->lchild = rRChild;
        } else {
            outerNode->rchild = rRChild;
        }
    }
}

// 右旋
void RRotation(TreeNode *tree) {
    /** 变量定义
     *     1(root)
     *     /
     *    2(rLChild)
     *   /   \
     *  3     0(orphan)
     *
     */
    TreeNode *root = tree;
    TreeNode *rLChild = root->lchild;  // (rootLeftChild)
    TreeNode *orphan = rLChild->rchild;
    TreeNode *outerNode = root->parent;

    /** 旋转
     *    2(rLChild)
     *   /   \
     *  3    1(root)
     *        /
     *     0(orphan)
     */
    rLChild->rchild = root;
    root->lchild = orphan;

    /** 父节点修正
     *   X(outerNode)
     *    ③
     *     ③双向修正
     *     2(rLChild)
     *     / ②
     *    /   \
     *   3    1(root)
     *        ①
     *        /
     *     0(orphan)
     */
    if (orphan)
        orphan->parent = root;    // ①
    root->parent = rLChild;       // ②
    rLChild->parent = outerNode;  // ③
    if (outerNode->data == -1) {
        outerNode->parent = rLChild;
    } else {
        if (outerNode->lchild == root) {
            outerNode->lchild = rLChild;
        } else {
            outerNode->rchild = rLChild;
        }
    }
}

第五节 红黑树删除

这部分要推导比较困难(主播是笨蛋!),建议直接记住;

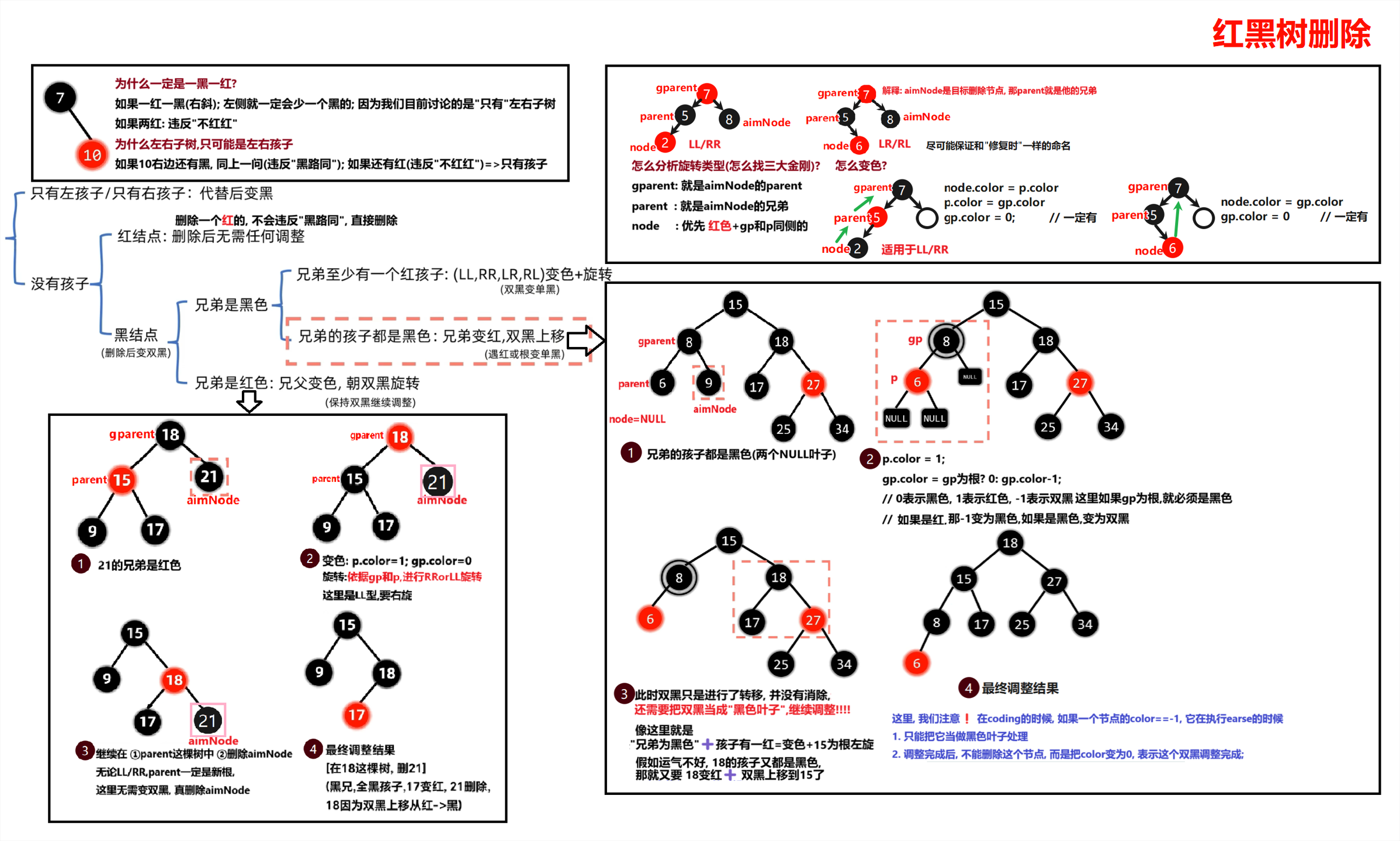
// 3.删除
void earse(TreeNode *root, int x) {
    TreeNode *aimNode = root;
    while (x != aimNode->data) {
        aimNode = x < aimNode->data ? aimNode->lchild : aimNode->rchild;
    }

    // case1: 叶子节点🍃
    if ((aimNode->lchild == NULL && aimNode->rchild == NULL) || aimNode->color == -1) {
        if (aimNode->parent->data == -1) {  // 细品(当前节点时根节点+当前节点是叶子==>整棵树只有一个根)
            aimNode->parent->parent = NULL;
            return;
        }
        // case1-1: 黑色叶子
        if (aimNode->color != 1) {
            /**  左侧情况 变量标识
             *   有两孩?优先左       没有左?就等于右       没有右,那为NULL
             *      a(gp)             a(gp)              a(gp)
             *     /  \              /   \               /   \
             *   b(p)  c(aimNode)   b(p)  c(aimNode)   b(p)  c(aimNode)
             *   /  \                 \
             * c(n) d                 c(n)               node=NULL
             */
            TreeNode *gparent = aimNode->parent;
            TreeNode *parent = gparent->lchild == aimNode ? gparent->rchild : gparent->lchild;
            TreeNode *node = NULL;
            if (parent == gparent->lchild) {
                if (parent->lchild && parent->lchild->color == 1)  //  优先同侧孩子
                    node = parent->lchild;
                else if (parent->rchild && parent->rchild->color == 1)
                    node = parent->rchild;

            } else {
                if (parent->rchild && parent->rchild->color == 1)  //  优先同侧孩子
                    node = parent->rchild;
                else if (parent->lchild && parent->lchild->color == 1)
                    node = parent->lchild;
            }

            // case1-2-1: aimNode兄弟为红色=>兄弟变为黑色;父亲变为红色;依据兄弟和父亲进行旋转;然后继续删除aimNode所在的树
            if (parent->color == 1) {
                parent->color = 0;
                gparent->color = 1;
                if (gparent->lchild == parent) {
                    // LL
                    RRotation(gparent);
                } else {
                    // RR
                    LRotation(gparent);
                }
                earse(parent, x);
                return;
            }
            // case1-2-2: aimNode的兄弟为黑色
            else {
                // 至少有一个红孩
                if (node != NULL) {
                    if (parent->data < gparent->data) {
                        if (node->data < parent->data) {
                            // LL
                            node->color = parent->color;
                            parent->color = gparent->color;
                            gparent->color = 0;
                            RRotation(gparent);
                        } else {
                            // LR
                            node->color = gparent->color;
                            gparent->color = 0;
                            LRotation(parent);
                            RRotation(gparent);
                        }
                    } else {
                        if (node->data < parent->data) {
                            // RL
                            node->color = gparent->color;
                            gparent->color = 0;
                            RRotation(parent);
                            LRotation(gparent);
                        } else {
                            // RR
                            node->color = parent->color;
                            parent->color = gparent->color;
                            gparent->color = 0;
                            LRotation(gparent);
                        }
                    }
                }
                // 一个红色孩子都没有
                else {
                    parent->color = 1;
                    gparent->color = gparent->parent->data == -1 ? 0 : gparent->color - 1;  // -1表示双黑,如果是根就为黑,红(1)--,也变为黑
                    if (gparent->color == -1)
                        earse(root, gparent->data);  // 双黑上移=继续删除gp的值 + 假删除
                }
            }
        }
        // case1-1: 红色叶子,直接删除,这条路上的黑色不会变化(不违反黑路同)
        if (aimNode->color != -1) {  // 如果是-1,表示为假删
            if (aimNode->parent->lchild == aimNode) // 注意删节点的方式: 和没有哨兵头的区别
                aimNode->parent->lchild = NULL;
            else
                aimNode->parent->rchild = NULL;
        } else {
            aimNode->color = 0;  // 修复为黑色即可
        }

    }
    // case2: 有两个孩子
    else if (aimNode->lchild != NULL && aimNode->rchild != NULL) {
        // 找到"中序遍历"的后继节点 (aimNode右子树的最左边节点)
        TreeNode *successor = aimNode->rchild;
        while (successor->lchild) {
            successor = successor->lchild;
        }
        // 换值(真, 因为只有真换值,才能保证aimNode的右子树是BST,才能使用earse方法继续删除)
        aimNode->data = aimNode->data ^ successor->data;
        successor->data = aimNode->data ^ successor->data;
        aimNode->data = aimNode->data ^ successor->data;

        // 删除右子树上的x
        earse(aimNode->rchild, x);

    }
    // case3: 只有一个孩子
    else {
        TreeNode *outerNode = aimNode->parent;
        TreeNode *son = aimNode->lchild ? aimNode->lchild : aimNode->rchild;
        // 修改颜色
        son->color = 0;  // 一红一黑; 用红替换了黑的,会少一个黑的,所以得替换
        // 修复父节点关系
        if (outerNode->lchild == aimNode) {
            outerNode->lchild = son;
        } else {
            outerNode->rchild = son;
        }
        son->parent = outerNode;  // 修改父子,双向修改
        // 替换 (没必要了, 修正父节点的子节点即可, 相当于完成替换了)
    }
}

第二章 手撕

第三章 相关应用

第四章 上手真题

第五章 比赛怎么用